【自我挑戰題-3】

 

1868：【更正版】國小低年級的超難數學題解答囉！

在書上看到相關的題目，所以就自己設計了底下這道題目，活化了很多人的腦細胞。

https://www.youtube.com/watch?v=fDdqp5_ZO80

也順便瞭解「國中生、高中生、大學生、研究生」等階段的學生們，對於這樣的題目會採取何種解決方式？

也因為「長的越大、學得越多」，很多同學們給我的答案與原理，就遠遠超出「國小低年級」的算法。

既然定義是「國小低年級」也可以算出答案。

所以，就不會是太難、太複雜的計算，主要的難度就在於「觀察規律」，而非難度設定在「計算方法」。

 

嘉義大學，大二學生「柯詩葦學姐」，是第一個完成作答傳給我的。也符合「一般學習、不超前進度的國小低年級」孩子可採取的方式。

「詩葦」學姐在國中階段，她就是上課時會反應、互動的學生。都念到大二了，依舊會有情有義的回到學校聊聊，值得你們學習。

 

 

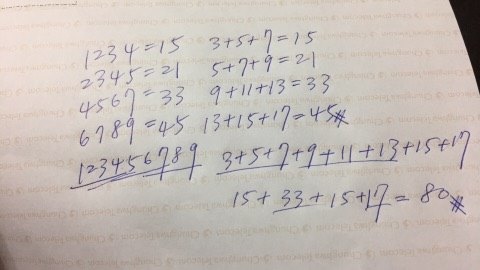
這次的結果有底下的狀況：

1.完全放棄者（只要看到數學二字，就完全不想動）

2.使用超出「低年級」程度的解題方式（乘法、除法、次方、小數點、排列、階層、..）

3.當作「腦筋急轉彎」、「飲料杯上的題目」看待者。

4.當作「哲學題目」看待者。

 

很正常，當我們學得越多就越難用適合該程度的方法去教導。

比方教一個國小，普通程度的學生，關於「雞兔同籠」的問題，

不可以用「未知數」的方式來解題時，你要如何教會他呢？

 

-----------------

補上「秀玲」與「冠叡」的解法，這樣也符合「國小低年級的程度」，所以增列上來。

 

 

感謝大家動動腦筋，這樣的討論可激發出更多的靈感，提供未來設計題目上的想法。

 

【資優數學挑戰題】TRML 個人賽 2004 第1題

 

考慮△ABC，D，E分別在邊AC、AB上，且BD與CE交於點P。若△BPE、△BCP、△CDP的面積分別為5、10、8，則四邊形AEPD的面積為？

 

 

 

 

 

 

 

 

 

 

 

 

 

【答】：22

【解析】x/5=y+8/10,y/8=x+5/10    x=10,y=12  合計：22

【資優數學挑戰題】TRML 個人賽 2003 第7題

如圖所示的四個相同半徑的圓互相外切且與邊長為6的正三角形相切。試求這些等圓的半徑長？

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

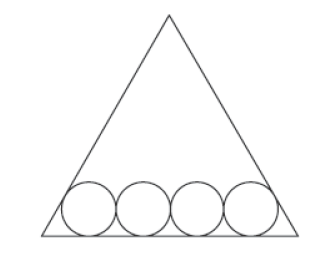
【答】：(3-√3)/2

 

【解析】√3r+6r+√3r=6   r=(3-√3)/2

 

【資優數學挑戰題】TRML 個人賽 2002 第5題

 

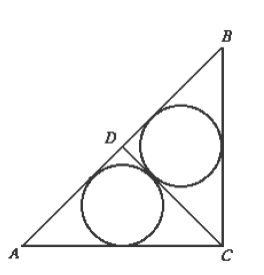
設△ABC中，∠C為直角，點D在斜邊AB上，AC=9，BC=8，CD=6。已知△ACD之內切圓與△BCD之內切圓有相同的半徑，試求△ACD與△BCD面積之比值。

 

 

 

 

 

 

 

 

 

【答】：15/14

 

【解析】△ACD: △BCD=AD:BD=AD+15:BC+14  ∴AD:BD=15:14

 

【資優數學挑戰題】TRML 個人賽 2002 第1題

試求最小的正整數，使其正因數的個數與108的正因數個數相同？

 

 

 

 

 

 

 

 

 

 

 

【答】：60

【解析】動腦想想，答案就出來囉！

【資優數學挑戰題】TRML 團體賽 2000 第7題

由阿拉伯數字1、4、7、8排成的四位數，每一個數字只能使用一次，試問其中有哪個數可表為四個連續偶數的平方和？

 

 

 

 

 

 

 

 

 

 

 

【答】：1784

【解析】動腦想想，答案就出來囉！

【資優數學挑戰題】TRML 團體賽 2000 第1題

【資優數學挑戰題】TRML 團體賽 2000 第1題

若多項式x^3-3x^2-6x+8 能被x-a及x+2a整除，試求所有可能的實數a的值。

 

 

 

 

 

 

 

 

 

 

 

【答】：1或 -2

【解析】原式=(x^3-x^2)-2(x^2+3x-4)=(x-1)(x^2-2x-8)=(x-1)(x+2)(x-4) 

【資優數學挑戰題】TRML 個人賽 2000 第2題

 

試求由阿拉伯數字5、6、7、8、9排成一個可以被11整除之五位數，每一個數字只能使用一次，試問其中最大的五位數為何？

 

 

 

 

 

 

 

 

 

 

 

 

【答】：98756

【解析】思考一下，應該就可想出來囉！

【資優數學挑戰題】TRML 團體賽 1999 第2題

在凸20邊形中，內角是銳角的總個數至多為何？

 

 

------，先動動腦，算出答案後，再看底下的解答---------

 

 

 

 

 

 

 

 

 

 

 

 

【答】：3

 

【解析】思考一個多邊形，外角最多可為幾個鈍角。

 

【資優數學挑戰題】TRML 個人賽 1999 第4題

設f(x)表領導係數為1之四次整係數多項式，而且f(1)=5,f(2)=10,f(3)=15,試求f(8)+f(-4)之值？

 

 

------，先動動腦，算出答案後，再看底下的解答---------

 

 

 

 

 

 

 

 

 

 

 

 

 

 

【答】：2540

 

【解析】

 

設f(x)=(x-1)(x-2)(x-3)(x-a)+5x
f(8)+f(-4)=210‧(8-a)+40-210(-4-a)-20=2540

 

 

【資優數學挑戰題】TRML 個人賽 1999 第一題

如圖，陰影部分S在以2為半徑之 1/4個圓中，而不在以2為直徑之2個半圓區域。試求S的面積？

 

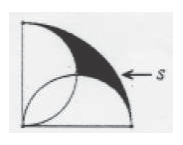
------，先動動腦，算出答案後，再看底下的解答---------

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

答：π/2-1

 

1/4‧2^2‧π-π+2(π/4-1/2)= π/2-1

 

 

【資優數學挑戰題】TRML 團體賽 2000 第1題

【資優數學挑戰題】TRML 團體賽 2000 第1題

若多項式x^3-3x^2-6x+8 能被x-a及x+2a整除，試求所有可能的實數a的值。

 

 

 

 

 

 

 

 

 

 

 

【答】：1或 -2

【解析】原式=(x^3-x^2)-2(x^2+3x-4)=(x-1)(x^2-2x-8)=(x-1)(x+2)(x-4) 

【資優數學挑戰題】嘉義高中 104 學年度科學班複試 第1題

嘉義高中104學年度科學班複試 第1題

設a,b為正整數。若a除以b的餘數是42，b除以42的餘數為12，則a與b的最大公因數為？

 

 

--------，先動動腦，算出答案後，再看底下的解答-----------

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

這一題比較簡單唷～

 

答：6

 

 

【資優數學挑戰題】嘉義高中102學年度科學班初試 第7題

 

 

--------，先動動腦，算出答案後，再看底下的解答-----------

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

【資優數學挑戰題】台中一中 104學年度科學班甄選入學試題 填充第10題

 

--------，先動動腦，算出答案後，再看底下的解答-----------

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

【資優數學挑戰題】嘉義高中97學年度 數理資優班成班複試 填充第2題