在書上看到相關的題目,所以就自己設計了底下這道題目,活化了很多人的腦細胞。
https://www.youtube.com/watch?v=fDdqp5_ZO80
也順便瞭解「國中生、高中生、大學生、研究生」等階段的學生們,對於這樣的題目會採取何種解決方式?
也因為「長的越大、學得越多」,很多同學們給我的答案與原理,就遠遠超出「國小低年級」的算法。
既然定義是「國小低年級」也可以算出答案。
所以,就不會是太難、太複雜的計算,主要的難度就在於「觀察規律」,而非難度設定在「計算方法」。
嘉義大學,大二學生「柯詩葦學姐」,是第一個完成作答傳給我的。也符合「一般學習、不超前進度的國小低年級」孩子可採取的方式。
「詩葦」學姐在國中階段,她就是上課時會反應、互動的學生。都念到大二了,依舊會有情有義的回到學校聊聊,值得你們學習。
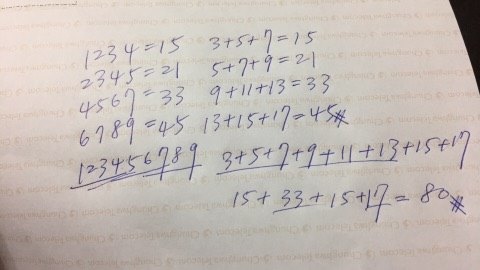
這次的結果有底下的狀況:
1.完全放棄者(只要看到數學二字,就完全不想動)
2.使用超出「低年級」程度的解題方式(乘法、除法、次方、小數點、排列、階層、..)
3.當作「腦筋急轉彎」、「飲料杯上的題目」看待者。
4.當作「哲學題目」看待者。
很正常,當我們學得越多就越難用適合該程度的方法去教導。
比方教一個國小,普通程度的學生,關於「雞兔同籠」的問題,
不可以用「未知數」的方式來解題時,你要如何教會他呢?
-----------------
補上「秀玲」與「冠叡」的解法,這樣也符合「國小低年級的程度」,所以增列上來。
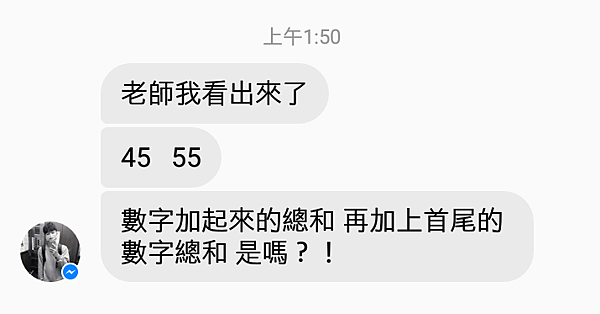

感謝大家動動腦筋,這樣的討論可激發出更多的靈感,提供未來設計題目上的想法。




沒有留言:
張貼留言